It was demonstrated that diffraction has an impact even at medium apertures.
Jim Kasson has a very nice example of that here:
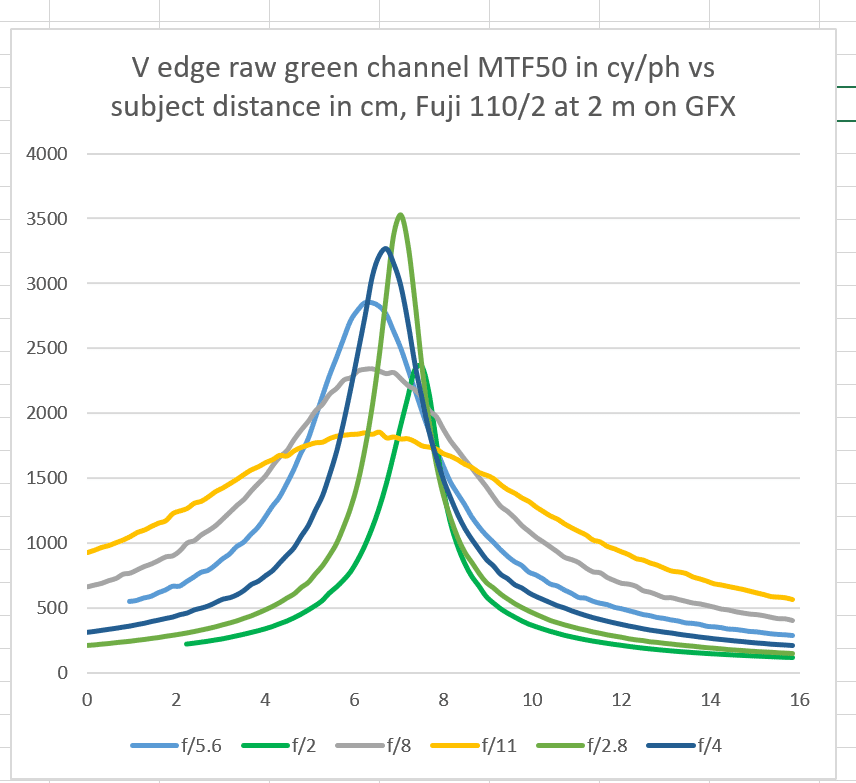
From Jim Kassons article :
https://blog.kasson.com/the-last-word/focus-shift-loca-of-fuji-1102-on-gfx/
This shows MTF 50 for the GFX 110/2 near axis at different apertures. We can see that the f/2.8 curve peaks at around 3500 cy/PH. That is the best such value I ever have seen. To some extent, it is due to the undersize microlenses on the GFX 50.
This also shows that stopping down to f/11 MTF 50 drops to around 1800 cy/PH. That is still a very reasonable value, Something like what I can get with my present gear at optimal aperture.
But, this is without sharpening. In the real life we always have some sharpening. I don't have Jim's raw images, so I demonstrate with some of my own.

This plots are from a test with my Sonnar 180/4 at f/5.6 and at f/11. Here we can see a significant loss of sharpness going from f/5.6 to f/11.

But, we can apply some sharpening, here I sharpened with FocusMagic using a radius of 2 for both images but using a different strength 50% for f/5.6 and 75% for f/11. So the images are pretty much similarly sharp up to like 2/3 of the Nyquist limit.
I would probably prefer sharpening with less halos, this is just a quick demo.
What would that mean in practice? When viewing the whole image say in projection at 4K or in a reasonably sized print, I don't think the difference between the two sharpened pictures would be noticable, as the left side of the MTF curve is essentially the same.
Looking at actual pixels, there may be a difference, but both are a bit too sharp.
Jim Kasson has some nice write up on best sharpening on the GFX 50 and the GFX 100,
but I cannot find it right now. Good stuff, if you can live with quite a few graphs.
Best regards
Erik