Lots of references to the exposure triangle (ISO/Shutter Speed/Aperture). Now, I am comfortable with the relationship between the 3 elements, but has anybody got a good explanation of how to use the triangle to define the relationship and how to use the triangle?
-
Welcome to the new forums! Please read this first. For known issues we are working to resolve, click here.
Exposure triangle explanation please.
- Thread starter AnthonyL
- Start date
The problem with that model is that it is very 2 dimensional. You can move along the ISO to Av points, or the Av to Tv points, but it doesn't show readily the three elements interacting. My model shows all three elements being pushed pulled, or if you hold the length of one element fixed, the other two must change.
With Auto ISO now becoming more prevalent a better visual model I think would be more helpful.
Lee
your apologies accepted. Lots of threads get messed up by noise. Only about 3 people have read my question and attempted to answer it. A lot of people have spent a lot of time answering a question I didn't ask. If people don't understand the question then don't answer it.
Beginners get quite confused about the relationship between ISO Tv and Av. Web sites show this triangle and then give an explanation which may just as well have not bothered about the triangle.
If you haven't yet got down to the post, see if http://www.dpreview.com/forums/post/51777903 makes any sense to you.
your apologies accepted. Lots of threads get messed up by noise. Only about 3 people have read my question and attempted to answer it. A lot of people have spent a lot of time answering a question I didn't ask. If people don't understand the question then don't answer it.
Beginners get quite confused about the relationship between ISO Tv and Av. Web sites show this triangle and then give an explanation which may just as well have not bothered about the triangle.
If you haven't yet got down to the post, see if http://www.dpreview.com/forums/post/51777903 makes any sense to you.
happysnapper64
Veteran Member
Anthony. I will have to read your triangle when I am not up to my eyes with painkillers, like Craig. I usually need to keep things as simple as possible. I have always used man & will try AV, & TV just to see how they work out. I have just changed metering modes, having used spot ever since I bought my camera. I have been so wrapped up in ISO, SS & aperture, that I never gave metering modes a second thought. I am using evaluative now [Canon] My next "adventure" will be to solve the mysteries of the 7D's AF system. Wish me luck :-D
Let S be ISO, t be shutter duration, N be f-Number. We'll call image brightness B where
B = log2(N^2/t) - log2(S)
The first term is the definition of exposure value, the second describes the effect of ISO on image brightness. What we want is B = log2(L/k) where L is scene luminance and a meter calibration constant. Manufacturers using slightly different values of k. Taking a logarithm,
B = 2*log2(N) - log2(t) - log2(S)
This how these *four* elements interact, and why a triangular graph paper labeled by powers of two establishes an 'exposure triangle' for a given level of incident light.
If you're trying to incorporate the third dimension of incident light, then you really do have a three dimensional object and can't express it as a triangle in two dimensions. You need an 'exposure pyramid'.
--
Jeff
http://www.flickr.com/photos/jck_photos/sets/
You don't make a photograph just with a camera. You bring to the act of photography all the pictures you have seen, the books you have read, the music you have heard, the people you have loved.” -- Ansel Adams
Last edited:
Gerry Winterbourne
Forum Pro
I've read the whole thread to this time. I recognise that you don't need a lecture on how the three parameters interrelate. However ...
... none of the ideas suggested actually provides an answer to the specific point of this question "how to use the triangle" if you mean for any practical use. There are several attempts, including your diagram, but what they all do is add some complexity to the conceptualisation of the three-way relationship.
The truth is that I can't imagine any way of actually using the triangle. To do so you'd have to put a scale on each parameter so that as you shorten shutter speed by one stop you have to widen aperture by one stop - assuming you keep ISO constant, of course.
You would actually need some sort of scaling that allowed you to move any pair (in unequal steps if that's what you want) in response to a change in the third. And you'd need to determine those scales according to the amount of light available.
In other words, the people who have said that the only use of the triangle is to show that there are three related parameters have got it right. The way to use it is to demonstrate this relationship.
The way to use it to define the relationships doesn't exist in any form simple enough to put into a straightforward diagram. Someone skilled in graphics and maths could no doubt build an interactive model that would move the three parameters as the light changed but it would be useless without a light meter built into it. Take away the interactive diagram and use scales instead and that's what a good old-fashioned light meter does. But it doesn't have any triangles.
robertorinehart
Leading Member
- Messages
- 551
- Reaction score
- 23
Nice explanation of the diagram. Thanks for the share!
clack
Forum Enthusiast
- Messages
- 288
- Solutions
- 3
- Reaction score
- 124
Look at the wooden triangle form the side so you see the three corners at equal distance dancing up and down.
Give each corner scale measuring ISO, Ts and A in the height variation of the corners
If you draw a series of bar graphs of the three values maintaining the same exposure value, you can draw in graph the balancing triangle as viewed from the side.
Yes I can see that as a good representation. All 3 corners can move, or if one corner is held fixed then the other two must "rock".
It would have the additional advantage of being quantitatively accurate if you made it horizontal slices through a pyramid with a triangular base, and where the height represented scene luminance.
JTC111
Leading Member
There is no use for the triangle as many people have pointed out to you already. You seem unwilling to accept that reality, so rather than waste time on that silly triangle, I thought I'd remind you of that which is more important: the photograph itself.
Limburger
Veteran Member
So you understand exposure.
Well, the relation between the three in the triangle is f-stops.
How using it is depending on what is important to you in a shot.
Do I need a high shutterspeed, 1/1000s for birds? Well that will be at cost of a higher ISO or larger aperture or even both in less than ideal situations. In case the scene has not much light upping the ISO is mandatory, though this at the cost of IQ (base ISO is what you want for best IQ). So there in this example only is aperture to play with to get your exposure right, this affects your exposure but DOF as well. Not much to choose.
If you only need a shutterspeed to prevent camerashake you can set a slower speed and may have more room to play with ISO and aperture. You shoot at 50mm eq. rule of thumb is 1/50s is enough (this may vary a little per person). Comes without saying that in this case I can shoot at a lower ISO and have some slack regarding aperture as well.
Aperture you can use for DOF in case it's desired to have just a certain amount, and ISO you basicly want as low as possible.
Short: a trade off when situations are less than ideal. In ideal situations you leave ISO at base and set shutter and aperture as desired.
In the filmdays they used higher ISO b&w film for grain (basicly that is make the image look worse) but it gave a nice effect to it.
I am no guru (just learning photography myself) but this is how I see it.
Just set everything so you get your subject correctly exposed,sometimes you can play with DOF other times you just have to do with available light.
--
Cheers Mike
Last edited:
Guidenet
Forum Pro
There we go. I real model, but how cumbersome to take into the field.
A folding tesseract might be even more accurate and at the same time more portable. Your tetrahedron using EV-L as the height but be better represented as just one aspect of our folding tesseract, don't you think? Nevertheless, you do have a working model ;-)
Last edited:
Limburger
Veteran Member
Plus ISO capabilities of your camera and aperture (a f1.8 gives you more room to play than a f3.5 lens).So gear can affect it as well. So good light may prevent hitting your gears limitations.
Just for some extra info, there's a forth force called the lighting control, especially in a controlled environment like a studio. Flashes, strobes, reflector.. they are all contributing to a proper exposure. Same triangle value, but EV will be affected by changing the fourth force.
Guidenet
Forum Pro
You're absolutely correct and several were calling it by it's normal term EV-L.
Jeff, in particular included it in his model.
Couldn't agree more. It doesn't simplify anything, the only grace is that it answers the OP's question.
Press Correspondent
Senior Member
You are trying to project a 3-dimensional formila to a plane. This is only possible as an illustration. Also the use of logarithms represents nothing, but the type of scale you have chosen. It is a complication that makes understanding dependent on the knowledge of logarithms tgat is not necessary.
Guidenet
Forum Pro
I think he has to in order to force this somewhat silly model to fit. Jeff knows it. Most of those expressions are those standardized definitions of exposure value needed to set it up. He's trying to show the need to incorporate EV-L or scene luminance. That's not going to be a triangle anymore, and if you continue, Jeff does a fairly good job of describing an accurate model I think. It's all not very useful, but does answer the question, don't you think?
Anyway, it looks just to be a fun attempt at meeting Anthony's request for a model. I certainly wouldn't want to take the time to close those expressions to an equation just to lose the logarithmic nature.
--
Cheers, Craig
Follow me on Twitter @craighardingsr : Equipment in Profile - f/22 Club Member
I reserve the right to make mistakes in reasoning and logic as well as to change my mind anytime I wish. I also ask forbearance with respect to my typos. Please take a look at my gallery here at DPR.
Last edited:
Press Correspondent
Senior Member
If I understand your question, it is about a graphical representation of the exposure values. You started with 3 values and therefore assumed a triangle. This assumption was the root of the problem of getting the correct answer. Then several users suggested the 4th parameter, the available light. It was a great insight, just not presented in the quantitative form. Finally, Jeff presented a formula, except reversed and unnecessarily overcomplicated. So let's get all this straight
The way I understand your question, it is about photographic CONTROLS, of which you started with the common 3. The 4th CONTROL is the amount of light. You can control it in a studio by the power of your lamps, but most commonly this is done by the automatic flash duration. Fir example, if you set your camera in a manual mode, but shoot with flash, the exposure is not set manually. It is still set automatically by the duration of the flash. Therefore in this example you can freely change all 3 of your common controls and still have the proper exposure. This has nothing to do with the amount of available light that you cannot CONTROL. Interestingly, one poster even mentioned a tesseract, which would represent the frame of reference for this case. However, for simplicity, let's stick to your original question and forget about the 4th control. This is the formula given by Jeff:
"Let S be ISO, t be shutter duration, N be f-Number. We'll call image brightness B where
B = log2(N^2/t) - log2(S)"
Well, actually the image brightness is proportional to the shutter duration, not reverse proportional. The same goes for ISO: the higher the ISO value, the brighter the output image is, nit vice versa. I am sure Jeff understands all this and these are not errors, but using a different convention. So let's simplify it.
Let A be the aperture control or the f-Number squared: A = N^2
Let T be the actual shutter duration (not the reversed one): T = 1/t (e.g. 0.03 sec = 1/30 sec)
Let S be sensitivity measured in the ISO numbers, such as 100, 1600, etc.
Then our brightness CONTROL number is:
B = A*T*S
Simple enough, now, where is the triangle here? Imagine 3 axes, X, Y, Z, just like in 3D graphs. They form a triangular pyramid of sort. This is as far as we can really go with the triangle analogy. Strictly speaking, a triangle is but a visual simplification (projection) of the 3D coordinates. There is no actual triangle there.
Then, what sort of a graph does this formula plot and what does it mean? In the A, T, and S axes, the formula creates a hyperboloid, a sort of smooth hill like surface. If we cut it with a plane by fixing any one of our 3 parameters as a constant (e.g. ISO = 100), then the cross section is a hyperbola or simply a reverse proportion (e.g. A*T = const or A = const/T or T = const/A, the dependences well known to any photographer and explained in this thread numerous times).
So here you go, the answer to your triangle question geometrically is a hyperboloid that looks cool and represents the well known dependencies among the exposure parameters. I hope this helps
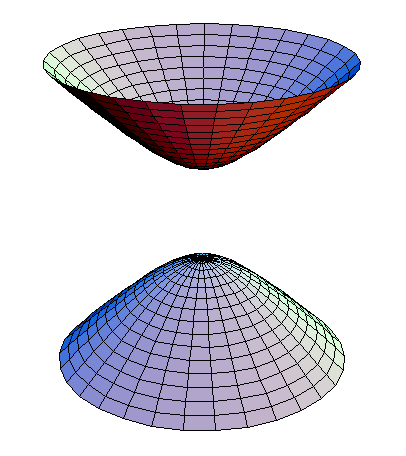
The way I understand your question, it is about photographic CONTROLS, of which you started with the common 3. The 4th CONTROL is the amount of light. You can control it in a studio by the power of your lamps, but most commonly this is done by the automatic flash duration. Fir example, if you set your camera in a manual mode, but shoot with flash, the exposure is not set manually. It is still set automatically by the duration of the flash. Therefore in this example you can freely change all 3 of your common controls and still have the proper exposure. This has nothing to do with the amount of available light that you cannot CONTROL. Interestingly, one poster even mentioned a tesseract, which would represent the frame of reference for this case. However, for simplicity, let's stick to your original question and forget about the 4th control. This is the formula given by Jeff:
"Let S be ISO, t be shutter duration, N be f-Number. We'll call image brightness B where
B = log2(N^2/t) - log2(S)"
Well, actually the image brightness is proportional to the shutter duration, not reverse proportional. The same goes for ISO: the higher the ISO value, the brighter the output image is, nit vice versa. I am sure Jeff understands all this and these are not errors, but using a different convention. So let's simplify it.
Let A be the aperture control or the f-Number squared: A = N^2
Let T be the actual shutter duration (not the reversed one): T = 1/t (e.g. 0.03 sec = 1/30 sec)
Let S be sensitivity measured in the ISO numbers, such as 100, 1600, etc.
Then our brightness CONTROL number is:
B = A*T*S
Simple enough, now, where is the triangle here? Imagine 3 axes, X, Y, Z, just like in 3D graphs. They form a triangular pyramid of sort. This is as far as we can really go with the triangle analogy. Strictly speaking, a triangle is but a visual simplification (projection) of the 3D coordinates. There is no actual triangle there.
Then, what sort of a graph does this formula plot and what does it mean? In the A, T, and S axes, the formula creates a hyperboloid, a sort of smooth hill like surface. If we cut it with a plane by fixing any one of our 3 parameters as a constant (e.g. ISO = 100), then the cross section is a hyperbola or simply a reverse proportion (e.g. A*T = const or A = const/T or T = const/A, the dependences well known to any photographer and explained in this thread numerous times).
So here you go, the answer to your triangle question geometrically is a hyperboloid that looks cool and represents the well known dependencies among the exposure parameters. I hope this helps
Guidenet
Forum Pro
heheheh.. you're as bad as the rest of us. What happened to EV-L?Press Correspondent wrote:
If I understand your question, it is about a graphical representation of the exposure values. You started with 3 values and therefore assumed a triangle. This assumption was the root of the problem of getting the correct answer. Then several users suggested the 4th parameter, the available light. It was a great insight, just not presented in the quantitative form. Finally, Jeff presented a formula, except reversed and unnecessarily overcomplicated. So let's get all this straight
The way I understand your question, it is about photographic CONTROLS, of which you started with the common 3. The 4th CONTROL is the amount of light. You can control it in a studio by the power of your lamps, but most commonly this is done by the automatic flash duration. Fir example, if you set your camera in a manual mode, but shoot with flash, the exposure is not set manually. It is still set automatically by the duration of the flash. Therefore in this example you can freely change all 3 of your common controls and still have the proper exposure. This has nothing to do with the amount of available light that you cannot CONTROL. Interestingly, one poster even mentioned a tesseract, which would represent the frame of reference for this case. However, for simplicity, let's stick to your original question and forget about the 4th control. This is the formula given by Jeff:
"Let S be ISO, t be shutter duration, N be f-Number. We'll call image brightness B where
B = log2(N^2/t) - log2(S)"
Well, actually the image brightness is proportional to the shutter duration, not reverse proportional. The same goes for ISO: the higher the ISO value, the brighter the output image is, nit vice versa. I am sure Jeff understands all this and these are not errors, but using a different convention. So let's simplify it.
Let A be the aperture control or the f-Number squared: A = N^2
Let T be the actual shutter duration (not the reversed one): T = 1/t (e.g. 0.03 sec = 1/30 sec)
Let S be sensitivity measured in the ISO numbers, such as 100, 1600, etc.
Then our brightness CONTROL number is:
B = A*T*S
Simple enough, now, where is the triangle here? Imagine 3 axes, X, Y, Z, just like in 3D graphs. They form a triangular pyramid of sort. This is as far as we can really go with the triangle analogy. Strictly speaking, a triangle is but a visual simplification (projection) of the 3D coordinates. There is no actual triangle there.
Then, what sort of a graph does this formula plot and what does it mean? In the A, T, and S axes, the formula creates a hyperboloid, a sort of smooth hill like surface. If we cut it with a plane by fixing any one of our 3 parameters as a constant (e.g. ISO = 100), then the cross section is a hyperbola or simply a reverse proportion (e.g. A*T = const or A = const/T or T = const/A, the dependences well known to any photographer and explained in this thread numerous times).
So here you go, the answer to your triangle question geometrically is a hyperboloid that looks cool and represents the well known dependencies among the exposure parameters. I hope this helps
--
Cheers, Craig
Follow me on Twitter @craighardingsr : Equipment in Profile - f/22 Club Member
I reserve the right to make mistakes in reasoning and logic as well as to change my mind anytime I wish. I also ask forbearance with respect to my typos. Please take a look at my gallery here at DPR.
Keyboard shortcuts
- f
- Forum