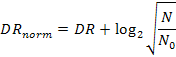boggis the cat wrote: If I shoot a scene and can capture a dark area (2, 3, 2, 3) through to a bright area (99, 100, 99, 100), then when I down-sample it to yield 2.5 through 99.5 I don't see this as having resulted in more of the scene becoming perceptible. It would be, on average, unchanged -- just less visible noise.
Momento, senor. In the full size original of our example, the darkest thing you dare print at brighter than full black "without" speckling, has a scene-brightness-value of more than 3. With the downsampling, the darkest values you can print are any values above 2.5. So you
really can see in a good-looking print, deeper into the shadows with downsampling. Or analogous multi-exposure stacking of a static scene.
boggis: Yes, but then you've dropped the highlights to 99.5 at the other end.
But if dynamic range is related to the brightness ratio of the lightest part of a scene, to the darkest clearly rendered part of the scene, that reduction due to downsizing of the darkest parts renderable, from more-than-3, to 2.5, in our silly example, is very significant. The brightest-to-darkest renderable scene value ratio goes from something over 33 (100 divided by something over 3) to around 40 (99.5 divided by 2.5, speaking very roughly).
What that more-darker-detail means is that the photographer
could for example, lighten that part of the final image, and more dark (albeit low-resolution) details could emerge, that would have looked as merely finely speckled noise before downsampling.
Usually, highlight detail is more noticeable (hence most important to photographers) than shadow detail. We're
usually not as bothered seeing blank black areas in a photo, than we are bothered seeing blank white areas. So usually a skilled photographer starts deciding exposure by turning down the exposure just enough that the brightest parts of a scene are rendered with detail.
The dynamic range of the imaging system then determines, for that important-highlight-preserving exposure setting, how much of the darkest parts of the scene can be rendered as smooth-looking, non-speckled shadow detail. If the dynamic range of the camera system is real narrow, and the darkest parts of the scene are "way darker" than the brightest important parts, the darkest parts of the scene will simply not have any recognizable detail in them that can be brought-out in post-processing by brightening. Because brightening those darkest parts will result in noise speckles rather than emerging dark detail.
But downsampling (or any other way of reducing shadow noise which is another way of talking about increasing dynamic range) gives the photographer the luxury of brightening the shadows (merely moving a shadow slider in Lightroom for example) without seeing speckled noise blotches emerge.
Basically, you have 'smoothed out' the photo -- blurred then down-sized it, in effect.
Not the worst description of "getting rid of noise", to say you've smoothed out the photo.
(And printing is a whole different matter, in any case. I am thinking of the captured data and how you can or cannot squeeze more information from it, prior to additional processing or printing. Different strategies such as hardware pixel-binning or multiple-exposures are a different consideration, and can obviously yield benefits in capturing the DR of a scene.)
Well by "printing" I meant preparing for final display on
some medium, which either your camera JPEG firmware does, and/or you the photographer are going to do in post-processing.
A big win is that you get to record and playback darker shadow values, without having to increase the exposure to dig out that greater shadow detail, thus blowing out the highlights to blank white.
That's getting a bit more complex. You're now into applying tone curves and such, when you are trying to preserve the highlights and lift the blacks.
Assuming the exposure was low enough to preserve highlight detail, dynamic range tells you how dark are the darkest parts of the scene that you'll be able to lift up in some kind of post-processing, to be made visible as dark detail in the final "print" or otherwse displayed image.
All that I wanted to establish was whether you really can get more DR from a captured photo -- the data -- by sacrificing resolution.
Yes. You give up peak resolution wherever you downsample, but the shadow noise speckling goes down nicely also. If you downsample from way 16 megapixels to 4 megapixels, ideally you will reduce the amplitude of the shadow noise by 2 (the square root of the downsampling ratio, 4).
It appears that this depends on what you mean by 'DR', but you can't 'unhide' actual DR by magically sweeping away noise
Now you're getting way over my head into sampling theory and statistics, but there's nothing magical about reducing shadow noise by downsampling. You reduce speckling as you reduce resolution. You're paying for your dynamic range increase with resolution decrease, it's not something for nothing.
downsampling doesn't exactly elevate or reduce the shadow values in the image file. What it does do it let you set the "black point" darker, i.e. with less dark-value noise you don't have to "pull down" the values of 3, 3.25 etc in post-processing (or indeed JPEG firmware) to pure black, just to bury the shadow noise speckling.
I don't see why you'd necessarily want to do that. If you were, for example, putting a 1:1 crop up on a website then yes, it may look bad unless you try to de-noise the shadow areas -- but routinely? I never bother, and haven't had any problems.
Check out this photo. If my camera had
infinite dynamic range, instead of its merely reasonable DR of about 9 exposure values or so, it would have been trivial for me to move the exposure slider and/or shadow slider upwards in Lightroom, and reveal more shadow detail. But instead I am forced to present the image to you with the darkest areas consigned to featureless black, since if lightened them they would at best be featureless gray (hence more obtrusive) and at worse super noise-speckled (even more obtrusive).
My own experience is that
almost every photo of every non-super-gray-scene is unable to be rendered with "all" its highlight detail, and "all" its shadow detail with my current gear. And I have to in almost every exposure just keep the exposure low enough to preserver highlights. Then in post-processing, futz with exposure, shadow and highlight sliders (in for example Lightroom) to tweak/optimize how bright in the displayed image or print to present the various dark and light parts of the original scene.
If you don't regularly have to do these things, then you either have a camera with more dynamic range capability than the dynamic range of the scenes you regularly photograph...or you are just quite lucky in that your default workflow and exposure-setting gear just always does an unassisted great job in both preserving highlights and not allowing dark parts of the scene to display as noisy speckled areas.
What I am really thinking of is how I want to know how much DR of an actual scene a camera can capture, and thus whether it is worth upgrading because, for example, DxO give a camera a larger number. If 'DR' is always a calculated 'engineering' value then that doesn't seem to necessarily help a photographer.
Well resolution is sort of a calculated value, but it's not just a mere engineering flight of fancy, it's a useful number that a whole bunch of us use to figure out what lenses to risk buying or trying.
Dynamic range really does tell you how contrasty a scene you can capture with clean shadow detail (or with great ISO-pushing-in-post-processing), in a single exposure at some certain resolution. Can't think of a scenario where more DR isn't better. The more DR, the less you have to worry about accidentally underexposing an image. I.e. the more you can err on the side of really well preserving the usually-more-important highlight detail.